Thinking about Algorithmic problems
In this posting we will discuss algorithmic thinking and try to propose a way of thinking that might become helpful when trying to solve a problem that does not have an obvious solution and some level of improvisation is required.
Based on my experience the three most important qualities of a programmer can be summarized as follows:
- Algorithmic thinking.
- Code design.
- Mastery of the language of choice.
The ability to solve problems that require the invention of a new algorithm combined with the skill of recognizing cases that can be solved directly by a “standard” one is one of the strongest signs of programming expertise and talent.
Although it is true that the need to create a brand new algorithm does not appear often in our days, it is also equally true that a programmer who has the ability to successfully combine analytic and synthetic thinking and efficiently solve a multi-dimensional problem will probably be proven to be more effective than somebody who does not.
Out of the three types of skills that I am mentioning above the one that requires the most programming talent is without a doubt the Algorithmic thinking; the most successful software companies are convinced about the the truth of this statement and this is why algorithms lie in the core of their interviewing processes.
Although talent is definitely required in most cases it is not enough when facing a new problem; we can certainly be assisted by some “methodical” steps that can serve as the blueprint for the creation of a solution and discussing them is the topic of this posting.
A summary of these “methodical” steps that I am usually following whenever I have to deal with an original problem is the following:
- Articulate the problem with clarity and try to understand niche cases.
- Creating several sets of testing input – output
- Code at least one brutal force solution
- Study the problem trying to understand it in depth.
- Decide if an existing algorithm can solve it directly or a special “trick” is needed;
- Can one of the standard methodologies like graph, recursion, dynamic programming or data structures can be used?
I will now pick a simple algorithmic problem and try to explain the thought process to solve it.
The problem
This is a well known problem that can be found in several websites that specialize on preparing candidates for programming positions.
Assume a water tank which has multiple parallel movable divisors placed in different locations as can be seen in the following picture:
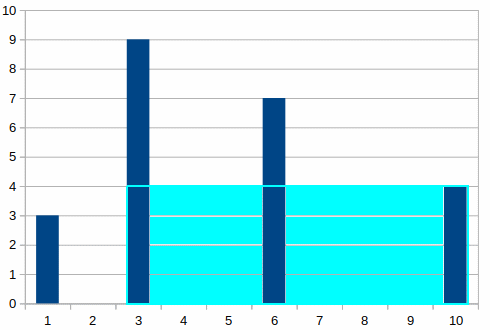
To better understand the picture you have to think that its third dimension is omitted; the blue bars represent the divisors that can be removed. Each divisor is set in a specific distance that cannot change.
The objective is to discover the two divisors that can hold the most water when others will be removed.
First thoughts
Now that we have the problem clearly defined, lets pause for a second and try to put together a trivial solution which will solve it without considering its performance.
The fact that we are looking for a pair of divisors makes it obvious that if find all the divisor pairs and calculate the covering areas for each of them and simply select the largest one (we do not need to consider the third dimension since it will be the same for all the pairs.
Before we do any coding and using the picture above we can create the testing data to check our brutal solution and verify it.
Eyeballing the picture we immediately see that there are two candidate solution:
The 1 – 10 pair results to 3 X 9 = 27 while the 3 – 6 pair to 7 X 3 = 21 so the expected solution will be 28.
Describe the problem programmatically
At this point it makes sense to try to describe the problem in a programming language (for this example we will use python).
The first thing that comes to mind is to represent the water tank programmatically. We can start by introducing a class to hold the coordinates of the upper point of each location:
import collections
Point = collections.namedtuple("Point", ['x', 'y'])
Now using Point we can represent the tank as follows:
tank = [Point(1, 3), Point(3, 9), Point(6, 7), Point(10, 4)]
Also we can declare the function to calculate the max_area:
def get_max_area(points):
pass
Since we already have calculated the expected answer we can add an assertion to validate our solution:
assert get_max_area(tank) == 28
At this point our code should look as follows:
import collections
Point = collections.namedtuple("Point", ['x', 'y'])
tank = [Point(1, 3), Point(3, 9), Point(6, 7), Point(10, 4)]
def get_max_area(tank):
pass
assert get_max_area(tank) == 28
If we run the program we should see the following output:

A Brutal solution
Assuming that we are having a pair of Points (representing two divisors) its covered area can be found if we multiply its width by the lower divisor:
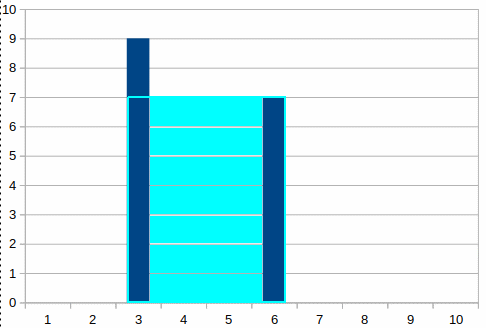
In this example the area will be covered by a 7 X 3 rectangle; 7 is the height of the lower divisor while 3 is the distance between them.
To simplify our solution, we can define a function which will receive two divisors as Points and return the enclosed area:
def get_area(p1, p2):
width = p2.x - p1.x if p2.x > p1.x else p1.x - p2.x
height = min(p2.y, p1.y)
return width * height
Now we are ready to implement the brutal solution. We should simply create all possible pairs of divisors, calculate the area for each of them and return the maximum value:
import collections
import itertools
Point = collections.namedtuple("Point", ['x', 'y'])
tank = [Point(1, 3), Point(3, 9), Point(6, 7), Point(10, 4)]
def get_area(p1, p2):
width = p2.x - p1.x if p2.x > p1.x else p1.x - p2.x
height = min(p2.y, p1.y)
return width * height
def get_max_area(tank):
max_area = 0
for p1, p2 in itertools.combinations(tank, 2):
max_area = max(max_area, get_area(p2, p1))
return max_area
assert get_max_area(tank) == 28
If we run the program above we will see that it completes without an error so our thought process was correct.
The problem with the brutal solution
Our brutal solution appears to be correct, so now let’s see how it scales. Let’s go ahead and stress test it by creating a tank that consists of a large number of points and see how it behaves. To do so we need to write a function to generate random points and call our get_max_area with increasing number of divisors:
import collections
import itertools
import random
import timeit
import functools
Point = collections.namedtuple("Point", ['x', 'y'])
def get_area(p1, p2):
width = p2.x - p1.x if p2.x > p1.x else p1.x - p2.x
height = min(p2.y, p1.y)
return width * height
def random_points(count, max_height):
for x in random.sample(range(1, count * 10), count):
y = random.randint(1, max_height)
yield Point(x, y)
def get_max_area(tank):
max_area = 0
for p1, p2 in itertools.combinations(tank, 2):
max_area = max(max_area, get_area(p2, p1))
return max_area
for count in [100, 1000, 5000, 10000]:
tank = list(random_points(count=count, max_height=12))
print(
'count:', count, 'duration:',
timeit.timeit(stmt=functools.partial(get_max_area, tank), number=1)
)
So, running the above program resulted on the following output on my computer:
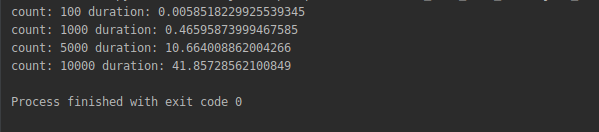
As you can see although our solution works fast enough when the number of divisors is low it grows very fast and when we are trying 10,000 of them it takes more than 41 seconds!
The poor performance is caused from the fact that we are calculating the area for all the possible pairs.
We now that the possible combination of n things by k are given by the following formula:
![]()
So assuming we have 10,000 divisors, the possible pairs will be:
![]()
which equals 49,995,000 or in other words it has a time complexity of O(C(n,k)) which results into an extremely slow solution.
At this point we must revisit our problem and think if we can come up with a “smart trick” that will allow us to improve our solution.. Please pause for a while and think our problem again trying to detect if there is something that will allow us to bypass most of the calculations of the brutal solution and then move on to the explanation of the efficient solution..
The trick
Lets revisit our original example and try to go step by step to an efficient solution. This time we will start by calculating the area of the first and last point as can be seen in the following picture:
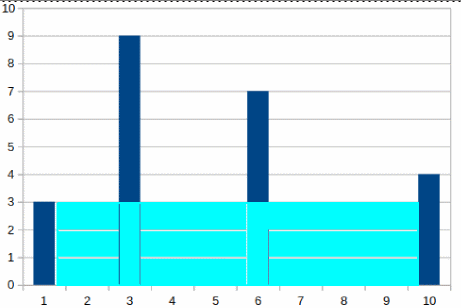
The area between the first and the last point is: 3 X (10 – 1) = 27.
Note that we use the point with the lower height and multiply it by the distance.
The trick arises is exactly here.
Note that for obvious the point with the lower height is impossible to result to a larger area when combined with any other point. This means that once we have calculated the first – last area in our example we can simply get rid of the first point without having to deal with it anymore.
This is a great improvement over the brutal solution since for it each point (including the first) has to be paired with all the others. In our example this means that for the brutal solution the first point is matched against all the three others but as we can see we do not need to do so since it is impossible to find a larger area anywhere else except the last point.
Following our observation, we keep the calculated area (27) remove the first point and continue to the next point as can be seen here:
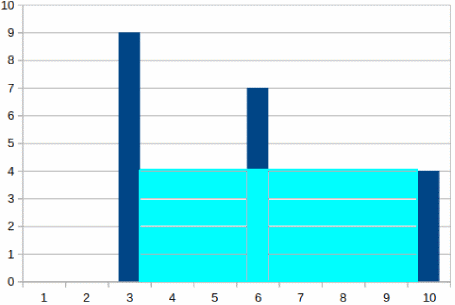
Note that now the last point is lower that the first; the enclosed area is 4 X (10 – 3) = 28 which replaces the previous maximum area value (was 27). Thinking in the same way we remove the last point and now our problem looks as follows:
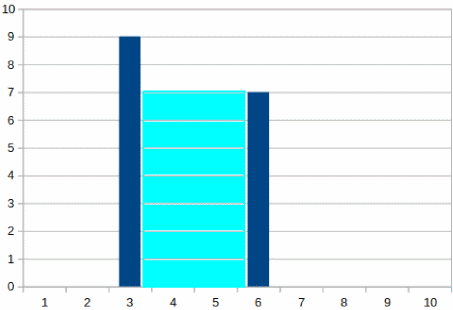
Now the enclosed area in 7 X (6 -3) = 21 which is less that the previous maximum area which remains 28 while we remove the lower Point and remain with a single point meaning that our problem is over and we have found the solution which is 28.
The efficient solution
Now that we have found the trick our next step is to re-write our get_max_area function replacing the brutal with the efficient logic:
def get_max_area(tank):
i1 = 0
i2 = len(tank) - 1
max_area = 0
while tank[i1].x < tank[i2].x:
height = min(tank[i1].y, tank[i2].y)
width = tank[i2].x - tank[i1].x
max_area = max(max_area, height * width)
if tank[i1].y > tank[i2].y:
i2 -= 1
else:
i1 += 1
return max_area
What happens here is simply expressing the steps we have followed before in python code.
* We start with two indexes pointing in the first and last point of the tank and we initialize the max_area to 0.
* Calculate the maximum area between the two indexes and store it if it is larger than the previous .
* Remove the lower point.
* Continue until the first point passes the second on the horizontal axis.
Now are full code including the testing data and the stress test becomes as follows:
import collections
import random
import timeit
import functools
Point = collections.namedtuple("Point", ['x', 'y'])
def random_points(count, max_height):
for x in random.sample(range(1, count * 10), count):
y = random.randint(1, max_height)
yield Point(x, y)
def get_max_area(tank):
i1 = 0
i2 = len(tank) - 1
max_area = 0
while tank[i1].x < tank[i2].x:
height = min(tank[i1].y, tank[i2].y)
width = tank[i2].x - tank[i1].x
max_area = max(max_area, height * width)
if tank[i1].y > tank[i2].y:
i2 -= 1
else:
i1 += 1
return max_area
tank = [Point(1, 3), Point(3, 9), Point(6, 7), Point(10, 4)]
assert get_max_area(tank) == 28
for count in [100, 1000, 5000, 10000]:
tank = list(random_points(count=count, max_height=12))
print(
'count:', count, 'duration:',
timeit.timeit(stmt=functools.partial(get_max_area, tank), number=1)
)
Running the program has the following output:
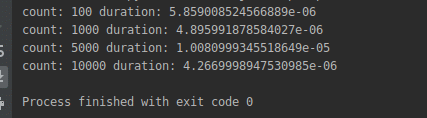
Note that now the 10,000 points are taking fractions of a second and compare it with the brutal solution to see how much faster this solution is.
The complexity of the efficient solution is O(n) meaning that for 10,000 points it will run approximately 10,000 times faster!
Concusion
In this article we have discussed an overview of the methodology to solve a problem with an unknown solution and how a programmer can tackle it by following a predefined number of steps that can be applied in almost every case. Further more we have discussed a specific problem and gave an ad-hoc solution that was superior to the obvious one which we had coded firstly. Going through the same process will be helpful for the most of similar scenarios.
